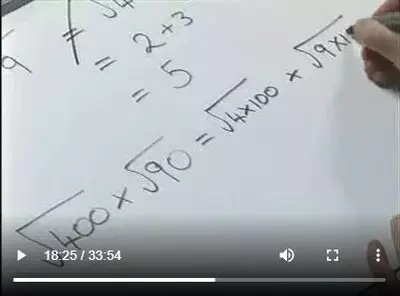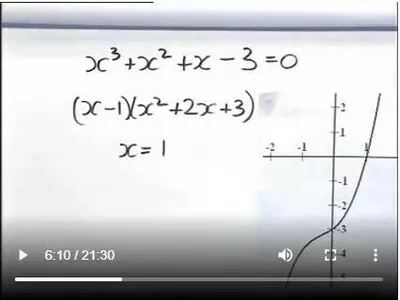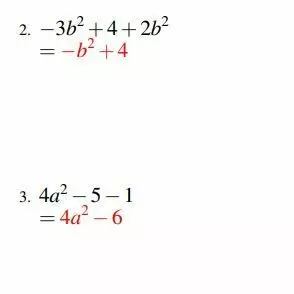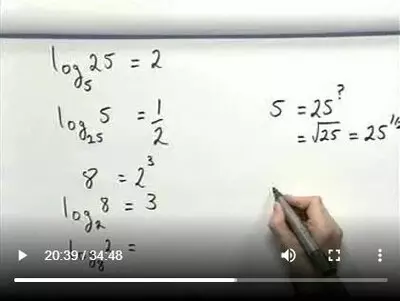High school
-
The Algebra ProjectThis 48 page booklet contains all the Algebra needed for Year 11 from Achieve (simplifying, expanding, substitution and solving) to Merit (simultaneous equations, factoring harder quadratics) to Excellence (quadratic sequences and complex equations). There are pages of drill and pages of examination questions. Can also be used for advanced Year 10 or Year 9.
-
-
Powers and IndicesPowers (also called exponents or indices) are a short way of writing multiplication of the same factor. A knowledge of powers, is essential for an understanding of most algebraic processes. In this video and PDF you will learn about powers and rules for manipulating them through a number of worked examples.
-
Simulations, Chance and DataA 60 page book with notes and handouts to guide through simulations showing that situations don’t always come out as expected. Can we predict male/female compositions in families? How many winning streaks can you expect when playing against a person of equal ability? How many packets of tea do you need to purchase in order to collect 6 jigsaw pieces? What floor will people get off from an elevator? Do lie detectors really work? What is the Monty Hall dilemma? Do we need to worry about radioactive decay? What are the chances of having the same birth date as another in a room? How fast can an infectious disease spread? Can we predict lambing rates on a farm? What are the chances of not getting on the plane on your next flight?
-
Year 9 ExamsThis booklet contains a sample Year 9 course outline as well as exams and practice exams for Year 9 and each of Terms 1, 2, 3 and 4. Problem solving, reasoning and communicating mathematical ideas are covered across all the strands of Number and Algebra, Measurement and Geometry, Statistics and Probability.
-
Year 9 Math HomeworkThis collection contains 40 weeks of 4 page homework sheets. Topics are introduced and revisited over the year. This involves mathematical processes such as problem solving, reasoning and communicating mathematical ideas. Topics include numeracy strategies, understanding numbers, confidence in calculating and the ability to estimate and approximate; recognising algebra patterns, thinking abstractly and communicating mathematical relationships; developing knowledge and understanding measurement systems with and without instruments, spatial awareness and using models as aids to solving practical geometry problems; collecting, organising, analysing, presenting and interpreting data; finding the probability of everyday events.
-
-
Year 10 Math HomeworkAs with the Year 9 math homework sheets this set contains 40 weeks of 4 pages for homework or general class use. The sheets constantly revisit topics with a lot of the work presented in practical and real life situations. Students may have never visited the Pantheon in Rome but that doesn't mean you can't enjoy some mathematical applications derived from this famous landmark, analyse data taken of Rooibus tea, a doctors appointment book or maths questions from the Prime Minister. When should you return to work after a hit on the head? mathematics around a garage, drawing and interpreting parabolas and expanding two sets of expressions in brackets. Everything you need for Year 10 maths is included in these sheets.
-
-
Simplify and SolveThis 82 page booklet contains work on simplifying expressions, exponents, solving simultaneous equations using algebra and graphs. The pages are ideal for Year 10 and Year 11 Algebra and specifically work for the "Apply Algebraic Procedures in Solving Problems" external examination.
-
Expand and FactoriseThis booklet contains 70 pages of worksheets (with answers) cover simple expanding and factorising through to harder work with quadratics. In most cases there are 5 parallel question papers that you can complete. It is an ideal Algebra resource for Year 10 students through to Year 11 especially those that want to sit the MCAT exam AS91027 Apply algebraic procedures in solving problems.
-
Year 11 Algebra SkillsThis resource can either be used to determine whether you have the algebra skills needed to proceed into a Year 12 mathematics course or it can also be used to study for AS91027 (the Level 1 MCAT - Maths Common Assessment Task). There are worked examples, practice questions, and practice assessments with all answers provided. Topics include indices, manipulating brackets, expanding and factorising, solving linear equations and other algebraic expressions. The booklet is 26 pages in length.
-
Years 9-11, Angle Geometry LessonThis PowerPoint covers angle definitions and properties for Year 9, 10 and 11. It includes angles on a straight line, in a triangle, interior and exterior angles of a polygon and parallel lines. The lesson should take approximately an hour from start to finish. All the answers are included in the PowerPoint and there should be time to discuss and explain each concept as you work through the slides. Ideal as a wrap up to an angles or geometry unit of work.
-
Encrypted MessagesThis is a PowerPoint designed for a one-off lesson on encryption. It features 3 encrypted messages. The first is a verse from Lewis Carroll's "The Hunting of the Snark", the second is an encrypted message that has 3 parts - the message itself, a hidden number inside the verse both of which then point to a planet in the solar system. The last is a 3 x 3 (9 letter) square where all the letters stand for a number. In each of the cases clues are given for students to decode the messages. Teachers should read the PowerPoint first as all the answers are contained in subsequent slides.
-
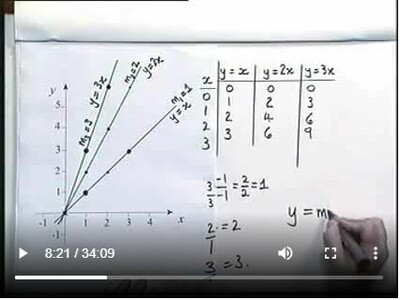
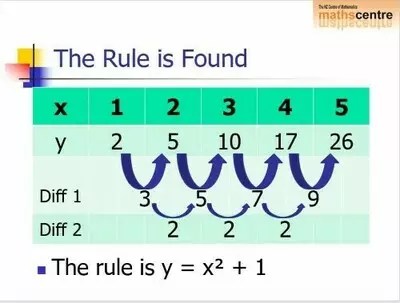
Quadratic PatternsThis 30 slide PowerPoint guides you through Linear Sequences and then shows you how to find the equation of a Quadratic Sequence of numbers
-
Miscellaneous WorksheetsThis resource was sent to us by Barry Bellamy, a retired NZ teacher. There are sheets on Angles, Area, Algebra - collecting like terms, Circle Geometry, Decimal arithmetic, Factorising, Fraction Arithmetic, Percentages, Solving Equations, Statistics (mean, median, mode, range), Substitution, Solving Quadratics, Standard Form, Transformations (enlargement, reflection, rotation).
-
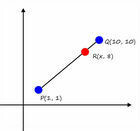
Coordinate Geometry (NCEA Level 2)AS91256 is a Year 12, Level 2 Standard worth 2 credits. This 40 page booklet provides a number of situations and problems that require you to find distances, lengths, gradients, midpoints, equations and perpendiculars. The questions contain scope for Achievement, Merit and Excellence type questions. There are many worked examples with lots of hints and tips. Full answers are supplied.
-
Straight LinesIf you don’t the understand the Level 2 Coordinate Geometry achievement standard then you should look at this booklet. It does not contain any exercises but does have a lot of worked examples to help you understand: The Distance Between Points, The Midpoint Formula, Gradients, Collinearity, Gradients of Perpendicular Lines, The Equation of a Straight Line, Medians, Altitudes, Perpendicular Bisectors, Intersection of Lines and Concurrency.
-
Systems of Equations (NCEA Level 2)AS91269 is a Year 12, Level 2 Achievement Standard worth 2 credits. This booklet provides a number of situations and problems that require you to form and use pairs of simultaneous equations and inequations. Both linear and non linear equations are used. There are 40 pages with many worked examples, lots of hints, tips and full answers.
-
LogarithmsBefore calculators logarithms were used to assist in multiplication and division. They still appear in a number of calculations in engineering, science, business and economics. There is a video that looks at what a logarithm is, why use it and examples on how to use them. There is also a PDF booklet with further information.
-
Year 12 and 13 Supplementary SheetsA 200 page workbook that can be combined into topic workbooks or used as supplementary work. Topics include: Expressions and Formula, Relations and Functions, Equations, Quadratics, Polynomials, Exponential Functions, Logarithms, Mid points, Parabolas, Circles, Ellipses, Hyperbolas, Conics, Sequences and Series, Binomial, Statistics, Trig Functions and Trig Identities. Answers are not provided.
-
CalculusIf you are having problems with Year 12 or 13 Calculus then read this 45 page booklet. There are no exercises but a lot of worked examples on Finding the Derivative, Differentiating with Respect to Other Variables, Rates of Change, Equations of Tangents, Increasing and Decreasing Curves, Stationary Points, Determining the Nature of Stationary Points, Curve Sketching, Closed Intervals, Graphs of Derivatives and Optimisation, Preparing to Integrate, Differential Equations, Definite Integrals, Geometric Interpretation of Integration, Areas between Curves and Integrating along the y-axis.
-
Year 13, Differentiating by First PrinciplesDifferentiation is about rates of change for example, the slope of a line is the rate of change of y with respect to x. To find the rate of change of a more general function, it is necessary to take a limit. This is done explicitly for a simple quadratic function.
-
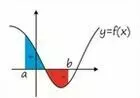
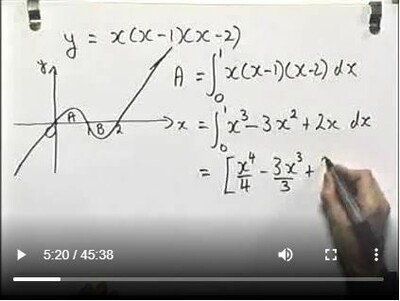
Year 13, Areas by IntegrationIntegration can be used to calculate areas under a graph. In simple cases, the area is given by a single definite but in more complicated cases the correct answer is obtained by splitting the area into several parts and adding or subtracting the appropriate integrals.
-
Year 13, The Quotient RuleThe quotient rule is a special rule that may be used to differentiate the quotient of two functions.
-
Graphs and GridsEver needed graph or log paper with different sized grids, a ready made set of axes for drawing lines, parabolas, hyperbolas or trigonometry graphs or some isometric lines or grids for drawing shapes? This 56 page booklet is the one for you. You will also find expanding circle templates, hexagonal and octagonal grids, 3 x 3 boxes for magic squares, fraction strips, fraction circles and squares, thermometers, protractors that can be printed onto clear plastic, number lines for integer arithmetic and 15 cm rulers that can be printed onto card.
-
SilhouettesWhat will be the odds? What does it mean when you read that heart attacks kill 1 in 5 people or that 1 in 8 women will get breast cancer? What does it look like when taken in context to a population? If taking a particular medicine improves the odds by 20%, how many will now survive? There are 4 pages in this document which give 200, 500, 1000 and 10,000 people silhouettes. They can be used in statistics exercises or by consultants to help illustrate what it actually looks like when given the odds.