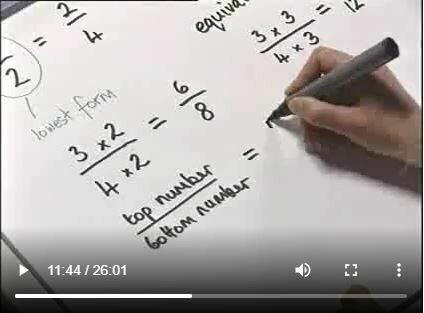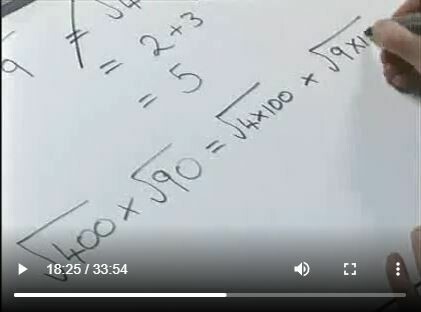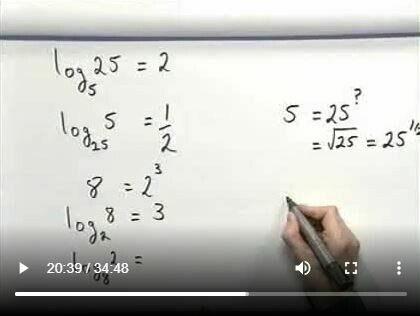Videos
Our team of top teacher mathematicians have put together all the important topics and explain them with the types of examples that you would find in a normal textbook or exam.
-
Year 7-10, Math Language
This video provides useful background material on the different mathematical symbols used in mathematical work. It also describes conventions used by mathematicians, engineers, and scientists. -
Years 7-9, Arithmetic Rules
Some mathematical sums are complicated, so rules have been established to make it clear which parts should be evaluated before others. This video covers the rules of precedence, adding, subtracting, multiplying and dividing. -
Years 7-9, Decimals
This video looks at decimals, and how they are related to fractions. It covers multiplying and dividing by 10, rounding to given numbers of decimal places or significant figures and finally looks at irrational numbers. -
Years 7-9, Fractions - Basic Ideas
What are fractions? What do fractions look like? What are equivalent fractions? What are the different types of fractions? This video explores all these concepts. -
Years 7-9, Fractions - Add & Sub
This video shows how to add and subtract fractions with the same denominators, different denominators and with mixed fractions. -
Years 7-9, Fractions - Mult & Div
This video shows how to multiply fractions and how to divide fractions by turning the second fraction upside down (called multiplying by the reciprocal). -
Years 7-9, Percentages
What is a percentage, how do you do calculations that involve percentages? How do you find a percentage? How do you calculate a percentage increase or decrease? This video covers it all and even shows you how to use the percentage button on a calculator -
Years 7-9, Ratios
A ratio is a way of comparing two or more similar quantities, by writing two or more numbers separated by colons. The numbers should be whole numbers, and should not include units. This video shows how to approach ratio problems. -
Years 9-10, Powers
Powers (exponents or indices) are a short way of writing multi multiplication of the same number. Knowledge of powers is essential to help understanding most algebraic processes. In this video you will learn about powers and rules for manipulating them. -
Years 9-10, Substitution and Formula
In mathematics, engineering and science, formulae are used to relate physical quantities to each other. They provide rules so that if we know the values of certain quantities, the values of others can be calculated. This video looks at several formulae and how they are used. -
Years 9-10, Expanding and Removing Brackets
Rewrite an expression in an equivalent form without any brackets then investigate the mathematics behind expanding and removing brackets using simple expressions through to nesting brackets (brackets inside other brackets). -
Years 9-10, Simple Linear Equations
This video is important for all Algebra students. It gives examples of simple linear equations and shows how the unknown quantity can be found. This involves collecting terms, removing brackets, and solving linear equations with fractions. -
Years 9-10, Simplifying Algebraic Fractions
This video explains essential work simplifying Algebraic Fractions. This involves simplifying fractions to their lowest equivalent form, fractions that need to be factorised before simplifying and then common mistakes made when cancelling. -
Years 9-11, Surds
Roots and powers are closely related, but some roots can be written as whole numbers. These are known as Surds. This video looks at how you can manipulate surds, simplify expressions involving surds and rationalising expressions involving surds. -
Years 10-11, Rearranging Formula
After viewing the video you should be able to: transpose formulae in order to make other variables the subject of that formula. It uses simple linear equations, the formula for the simple pendulum and further examples of useful formulae. -
Years 10-11, Pythagoras
The square on the hypotenuse is equal to the sum of the squares on the other two sides. In this tutorial we revise the theorem and use it to solve problems in right-angled triangles. -
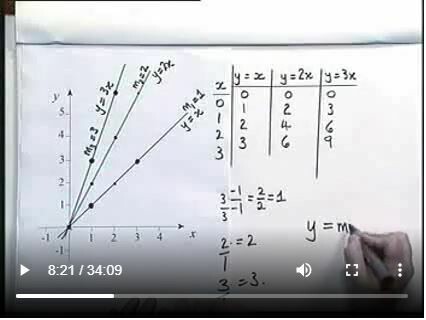
Years 10-11, Equations of Straight Lines
In this unit the equation of a straight line is established using either information about its gradient together with the co-ordinates of a point on the line, or alternatively the co-ordinates of two different points on the line. The different ways of expressing the final equation are explored. -
Years 10-11, Solving Simultaneous Equations
Solving a pair of simultaneous equations is equivalent to finding the intersection point of two straight lines This video looks at the main methods of solving simultaneous linear equations - elimination, substitution and then looks at further examples and how to approach them. -
Years 10-11, Solving Inequalities
This video explains linear and quadratic inequalities and how they can be solved both algebraically and graphically. It includes information on inequalities in which the modulus symbol is used. -
Years 10-11, Factorising Quadratics
Factorising is the process used to 'remove' brackets from an expression. This video looks at factorising by inspection and then by other methods when the x2 coefficient is >1 or when there is no constant term. -
Years 11-12, Trig - Right Angled Triangles
Trig ratios in a right angled triangle Knowledge of these trigonometric ratio: sine, cosine and tangent is vital in many fields of engineering, science and maths. This unit introduces them and provides examples of how they can be used to solve problems -
Year 11-12, Trig Ratios of Any Angle
Trig ratios of an angle of any size. Knowledge of the trigonometric ratios sine, cosine and tangent is vital in many fields of engineering, math and science. This unit explains how the sine, cosine and tangent of an arbitrarily sized angle can be found -
Years 11-12, Solving Quadratics
This video is all about finding the solutions of quadratic equations. These take the form ax2+bx+c = 0. It looks at four methods: factorisation, completing the square, using a formula, and finding the solutions by using graphs. -
Years 11-12, Completing the Square
Quadratic expressions can be written in an equivalent form using the technique known as completing the square. This video explains the basic ideas behind completing the square and how to use the method to solve quadratic equations. -
Year 12, Trig - Non Right Angled Triangles
A common mathematical problem is to find the angles or lengths of the sides of a triangle when some, but not all, of these quantities are known. It is also useful to be able to calculate the area of a triangle from some of this information. -
Year 12, Gradient of a Straight Line
This video explains how to find the gradient of a straight line, and the relationships between parallel lines and perpendicular line gradients. After viewing the video you should be able to: calculate the gradient of a line through two points; use gradients to determine whether two lines are parallel; use gradients to determine whether two lines are perpendicular. -
Year 12, Finding Maximums and Minimums
A derivative provides information about the gradient of a graph. Such points are often associated with the largest or smallest values of the function, In many applications, scientists, engineers, or economists are interested in such points for maximising power, or profit, or minimising losses or costs. -
Year 12, Completing the Square to Find Max and Min
Completing the square has several applications including the solution of quadratic equations. In this video we use it to find the maximum or minimum values of quadratic functions. -
Year 12, Logarithms
Before calculators logarithms were used to assist in multiplication and division. They still appear in a number of calculations in engineering, science, business and economics. This video looks at what a logarithm is, why use it, and examples on how to use them. -
Year 12, Solving Cubic Equations
Cubic equations have either one real root, or three real roots. In this video we explore why this is so, how to solve them to find the roots and how to use graphs to solve them. -
Year 12, Properties of Straight Lines
In this unit a system of co-ordinates is described, and is used to find various properties of the straight line between two points. The distance between the two points and the mid-point of the line joining the two points are calculated. -
Year 12, Arithmetic and Geometric Progressions
After the video you should be able to: recognise the difference between a sequence and a series; recognise an arithmetic or geometric progression; find the nth term of a progression; find the sum of an arithmetic or geometric series; and find the sum to infinity of a geometric series with common ratio |r| < 1. -
Year 12, Sum of an Infinite Series
After viewing the video tutorial on this topic, you should be able to: recognise the difference between a sequence and a series; write down the sequence of partial sums of an infinite series; determine (in simple cases) whether an infinite series has a sum. -
Year 13, Differentiating from First Principles
Differentiation is about rates of change for example, the slope of a line is the rate of change of y with respect to x. To find the rate of change of a more general function, it is necessary to take a limit. This is done explicitly for a simple quadratic function. -
Year 13, Areas by Integration
In simple cases, areas can be found by evaluating a single definite integral. Sometimes the integral gives a negative answer, and sometimes the correct answer can be obtained only by splitting the area into several parts and adding and subtracting appropriately. -
Year 13, Product Rule
The product rule, exists for differentiating products of two (or more) functions. This video explains and shows examples of this rule. -
Year 13, Quotient Rule
This video explains and gives examples of the quotient rule. This is a special rule that may be used to differentiate the quotient of two functions. -
Year 13, The Chain Rule
The chain rule is a special rule that may be used to differentiate a composite function (that is, a function of another function). This video explains the concept and gives examples -
Year 13, Conic Sections
Conic sections are curves resulting when a cone is cut by a plane. One of these curves, the parabola, is found using an alternative description in terms of points whose distances from a fixed point and a fixed line are equal. -
Year 13, Trig Identities
Some important identities derived from a right-angled triangle are: sin² A + cos² A = 1; sec² A = 1 + tan² A and cosec²A = 1 + cot²A. This video shows how to usie these identities to solve equations -
Year 13, Solving Trig Equations
The strategy we adopt in solving trigonometric equations is to find one solution using knowledge of commonly occurring angles and then use the symmetries in the graphs of the trigonometric functions to deduce additional solutions -
Factors - Introduction
A factor is a number that divides another number, leaving no remainder. If two whole numbers multiplied gives us a product, then the numbers we are multiplying are factors of that product. -
Factors - Highest Common Factor
Learn all about the HCF (Highest Common Factor) of two numbers. It is the highest number among all the common factors of the given numbers -
Multiples - What Are They?
A multiple is the result of multiplying a number by an integer (not a fraction). This video will take your through Multiples - a definition and some examples of multiples. -
Multiples - Lowest Common Multiple
List the multiples of each number, circling any common multiples. The lowest one is the lowest common multiple (LCM). -
Number - Decimals
All about decimals and how to round them -
Exponents - Introduction
As we get further into math concepts you will will recognise numbers with little numbers above to the right. These are also called powers or indices. This video explains what they all mean and how you can use them. -
Integers - Introduction
An integer is a whole number (not fractional) that can be positive, negative, or zero. This video explains about integers and gives some real life example of their use. -
Exponents - Common Exponents
Often in math we come across common exponents. This video explains what an exponent is, what the common exponents are and what they mean. -
Integer Comparisons
This video compares smaller and larger numbers by the use of a number line. For a complete unit of work on Integers go to the Middle School section. -
Algebra Substitution
What is substitution, why do we do it and how do we do it? -
Algebra - Expanding Brackets Overview
In Algebra, what does expanding mean and how do we do it? -
Algebra - Expanding Single Brackets
How do you expand a single bracket? -
Algebra - Expanding a Single Bracket with a Negative Term
What happens when expanding becomes a little more complex and uses negative numbers?